How atmospheric seeing affects telescopes with different focal ratios

Home

Telescope Thermodynamics

Sept. 2000 Sky & Telescope magazine companion web site

May & June 2004 Sky & Telescope magazine companion web site

Using fans with a Newtonian telescope

Tips on attaching a temperature probe to your telescope

Optical Miscellany

Try this at home!

How atmospheric seeing affects telescopes with different focal ratios

Animated focal plane illumination map

Properties of various mirror substrate materials

Adventures in collimation

Introduction

Disturbances in the atmosphere refract the light from a star in the same manner as a lens. Ideally, the incoming wave front from an infinitely distant source is perfectly flat. The effect of a disturbing "air lens" is to cause the wave front to be warped, and there is a small shift in the position of best focus (i.e., the focal plane).

It is well understood that telescopes with a higher f-number have a greater depth of focus. From a practical standpoint, this means high f-number telescopes are easier to focus, since there is a generous region of focus travel where the image is essentially optimal.

It is sometimes claimed that for telescopes of equal aperture, but different focal ratios, the longer focus instrument will perform better for a given atmospheric condition. Presumably, this is because the focus shift caused by the atmospheric cells is better absorbed by the greater depth of focus of the longer telescope. This hypothesis is tested below by two independent methods; 1) a ray trace analysis, and 2) by a depth-of-focus analysis using established formulae.

Ray Trace Analysis

Perhaps the most direct method of testing this hypothesis is by modeling two telescopes in an optical ray tracing program. Computer programs such as Zemax® and OSLO® not only model geometric rays, but also predict the diffraction performance characteristics of optical systems. Optical parameters like the point spread function (PSF) can be calculated, along with other useful parameters like the modulation transfer function (MTF) graph and the Strehl ratio. PSF, MTF, and Strehl ratio are intrinsic performance measures, and are directly related to what we actually see with our eyes. I have chosen to compare the PSF, since it is the simplest to represent and understand (the PSF is essentially the familiar startest pattern). Since the modeled telescopes will be optically perfect, any PSF value less than 1.000 will be due to the atmosphere alone.

For this example, two 150 mm aperture telescopes — a f/5 and a f/10 — were modeled in OSLO. Figure 1 shows the PSF plot and values for both of these perfect systems under ideal skies. Not surprisingly, both have identical on-axis PSF values of 1.000 (indicating perfect on-axis performance).

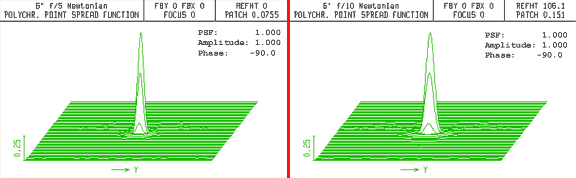
Fig. 1. Point spread function comparison of the f/5 and f/10 telescopes with perfect optics and no atmospheric turbulence.

To mimic a cell of disturbing atmosphere, a weak plano-convex lens is placed about 5 miles (8 x 10⁶ millimeters) above the telescopes. Figure 2 shows the PSF for both telescopes is degraded by the same amount (to 0.658). Repeating this for any power of atmospheric "lens" has the same effect; the PSF for both instruments is identically affected. (Note: If you simulate this yourself, do not optimize the focus position between trials. This would be like refocusing the eyepiece to accommodate for bad seeing.)

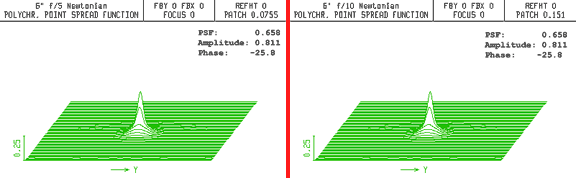
Fig. 2. Point spread function comparison of the f/5 and f/10 telescopes with the same "air lens" 5 miles above them.
The PSF is affected the same in both instruments. The telescopes were not refocused.

The real atmosphere can be modeled as an infinite number of lensing effects. Since all of these can be linearly added, the principals of superposition permit the results of this one test to be carried into the more complex reality. If you want to validate this test on your own software, the exact designs I used can be viewed here.

Depth of Focus Analysis

An independent method that corroborates the previous ray tracing result is to calculate the depth of focus for the two telescopes, and compare it to the shift in the best focus position that is induced by bad seeing. Sidgwick(1) provides a formula for calculating the depth of focus as:

depth of focus = 4*(1.22*lambda*(F²))

where;

F = focal ratio

lambda = wavelength of light.

This formula, and similar ones, are also mentioned by Suiter(2). The important thing to note is that the depth of focus changes with the square of the focal ratio, F. Thus, a f/10 telescope has four times the depth of focus of a f/5 instrument (i.e., (10/5)²).

This looks good for the long focus telescope until you also look at how much the atmosphere affects the focus shift for the two telescopes. Table 1 shows the amount of best focus shift for three different "air lenses" of varying optical power. OSLO was used to derive these numbers. The important thing to notice is that the f/10 telescope has four times more focus shift than the f/5. In fact, this focus shift varies by the same ratio as the depth of focus does — the ratio of the focal ratios squared. This exactly neutralizes the benefits of the greater depth of focus.

Table 1. Shift in best focus for atmospheric "air lenses" of varying strength.

Conclusion

Telescopes of equal aperture are affected the same by atmospheric turbulence, regardless of focal ratio. The error in the hypothesis is that it was assumed that the same atmospheric distortion will cause the same shift in the best focus position in the two telescopes, and this is not true. While the high f-number telescope does enjoy a greater depth of focus, unfortunately the shift in best focus caused by turbulence is also greater. In fact, the two are locked together; the instrument with four times greater depth of focus also has a four times greater linear shift of the best focus position.

There is a long list of valid reasons why high f-number telescopes often perform better than faster ones. Some important reasons are:

a) Slower (i.e., high f-number) optics are exponentially easier to fabricate to the same accuracy as faster optics.
b) As already mentioned, the greater depth of focus of the high f-number telescopes makes them easier to precisely focus.
c) High f-number telescopes have a larger region of the focal plane that is diffraction limited, so off-axis performance is better. This is especially true with Newtonians, where coma and eyepiece astigmatism (mostly the latter) can be noticeable off-axis problems in fast instruments.
d) Slower optics are easier to collimate accurately, and there are less detrimental optical implications to slight misalignments.
e) Many eyepieces perform better with a higher f-number.
f) When comparing two Newtonian reflectors, slower scopes usually have smaller secondary mirrors. While the difference in image quality between, say, a 15% and 20% obstructed telescope is hard to detect, it would be a contributing factor.

If you happen to be observing through two telescopes of the same aperture on the same night, and the longer focus telescope is performing better, some of the reasons stated above are likely to be the explanation. Also, are the two scopes you're comparing of the same design type (i.e., reflector, refractor, SCT)? If not, they most likely have different thermal behaviors.

References

(1) Sidgwick, Amateur Astronomer's Handbook, 4th ed., page 425

(2) Suiter, H. R., Star Testing Astronomical Telescopes, 3rd ed., page 79

Return to Telescope Optics Topics.